2021/9/5 UPD: 更新了多叉分治半在线卷积的模拟。。。

简介

阅读了参考文献后感觉这种方式是不是比较好理解（图片基本来自 Hoeven 的论文，倍增的想法在 EI 和 Athekatelan 的论文中有描述），所以写 复读 了一下，有错误感谢指出！

考虑多项式 $f=\sum_{i=0}^{n-1}f_iz^i,g=\sum_{i=0}^{n-1}g_iz^i$ 且现在只考虑 $f,g\in\mathbb{F} _ {998244353}[[z]]$ 那么将 $fg$ 描述为下面的正方形如

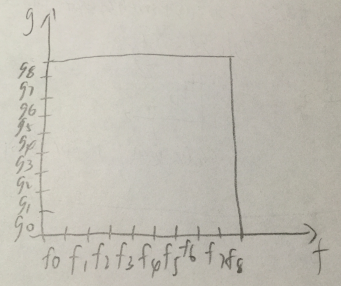
在线卷积是说当 $f_i,g_i$ 给出后立即给出 $(fg)_i$ 我们令 $P=fg$ 那么意思就是假设给出了一个 $f_8,g_8$ 那么实际计算的是

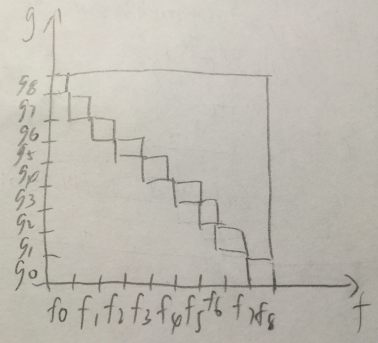
就是这个对角线上这些方块对 $P$ 的贡献（一个对角线就贡献在 $P$ 的同一处），很容易发现这是朴素算法，朴素算法是在线的。但是我们观察到当 $f_8,g_8$ 给出后，我们可以计算的是整个正方形对 $P$ 的贡献，而不仅仅是这一条对角线上的东西，这指导我们对该大正方形进行划分，划分为比 $1\times 1$ 的更大的正方形，然后一个正方形可能可以用一次离线/半在线卷积来计算，下面介绍一种很显然的倍增的划分方式。

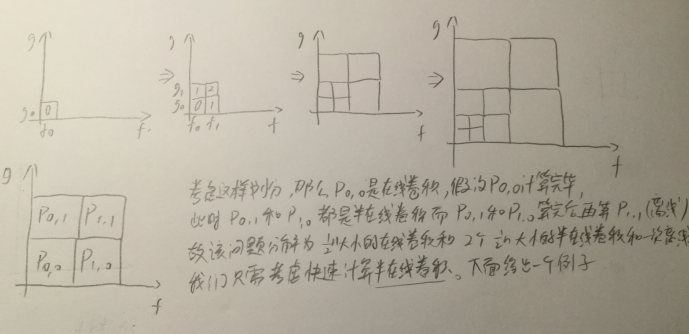
考虑这样划分，那么 $P_{0,0}$ 是长度为一半的在线卷积，假设 $P_{0,0}$ 计算完毕，此时 $P_{0,1},P_{1,0}$ 为两个长度一半的半在线卷积，而 $P_{0,1},P_{1,0}$ 计算完毕后，我们离线计算 $P_{1,1}$ 因为 $P_{1,1}$ 对于当前要求的系数是没有贡献的。下面给出一个半在线卷积的例子，可以很方便的写出迭代算法

假设 $g$ 已经离线给出，而 $f$ 的系数在线给出，那么步骤可以是

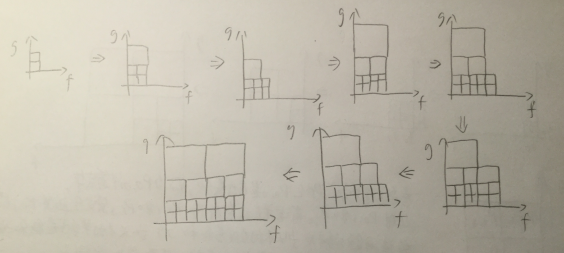
很容易发现这就和分治法是一样的（每一个正方形都可以离线计算），使用正方形描述使得写出一般的迭代算法看起来也并不复杂，且我们使用倍增方法的在线算法调用的半在线算法大小必然是 $2$ 的幂次。时间为 $O(n\log ^2n)$ 。

下面是我的一个想法，我们创建一个在线卷积对象，其只需持有 $f,g$ 的指针和两个半在线卷积对象的指针和一个贡献数组，然后有一个 next 方法返回下一个系数（只要 $f_i,g_i$ 已经填充完毕就能计算 $(fg)_i$ ），调用后调用两个半在线卷积的 next 方法去给贡献数组算贡献，长度到 $2$ 的幂次后进行一次离线卷积算完这个正方形，然后倍增长度，如此便获得了一个简单的在线算法。

多叉分治半在线卷积 via Middle Product 简单理解

Middle Product 即循环卷积的转置，但因为论文在转置原理的论文之前发布，所以这个称呼一直沿用了下来。简单来说我们可以使用循环卷积求出下图阴影部分中的贡献，其转置也可以求，但绕了个弯，没必要使用。下面我们考虑 $g$ 的系数离线给出，而 $f$ 的系数在线给出。

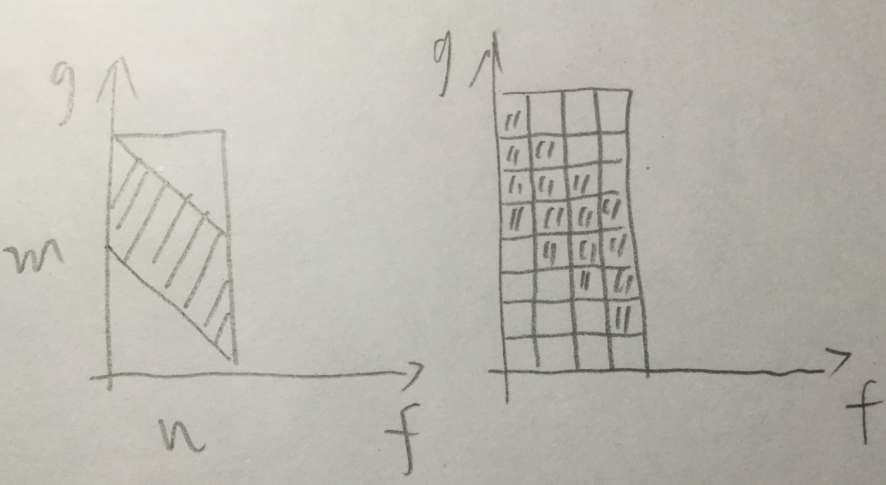
左图是粗略的表示，右图为 $n=4$ 时真实的表示。我们考虑四叉分治（更多叉分治也是类似的，但不便于模拟），那么模拟如下

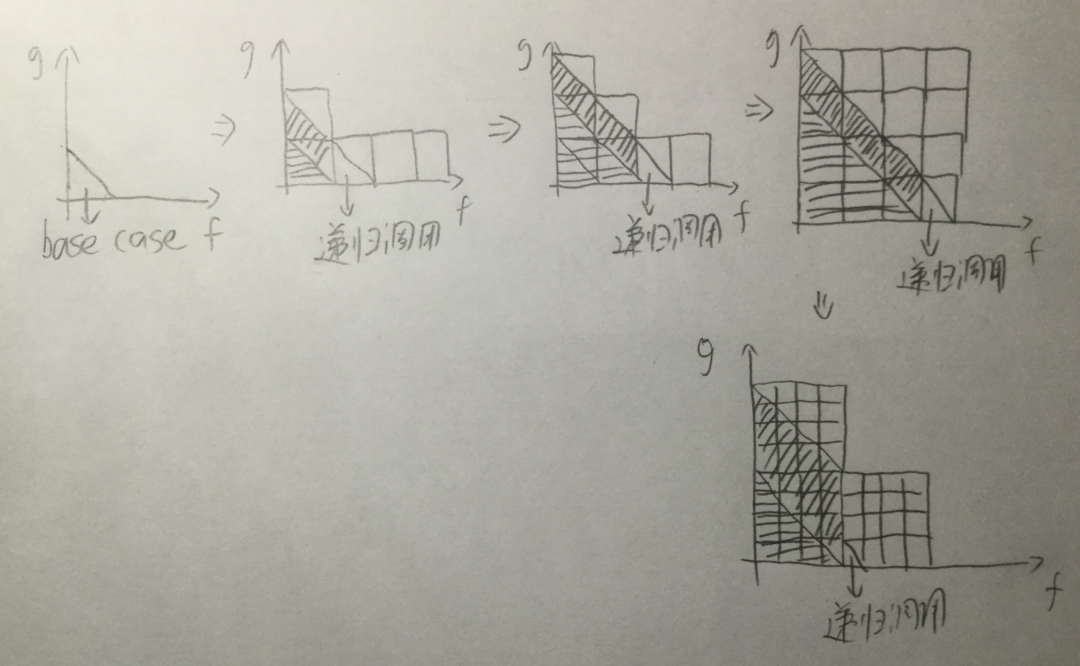
其中横线的阴影部分为之前计算完毕的，而斜线的阴影部分为当前需要计算的部分。

通过上述模拟我们写出递归代码是轻而易举的，这也正是现在使用最广泛的多叉分治实现幂级数指数函数较快且相当简单的写法，通过对算法的模拟，我们可以更容易编写迭代算法，而两个同步进行的半在线卷积就得到了在线卷积的算法（如果不需要同步进行，那么可以编写递归的算法）。但与 Hoeven 论文中不同的是，我们没有将贡献分解为正方形而是三角形和平行四边形，所以在线卷积在完成了其中的半在线卷积后需要根据需要补全一下。这也正是所谓的计算前半部分对后半部分的贡献这一说法，只不过看起来没那么抽象。。另外我发现使用 Middle Product 进行的半在线卷积改造成在线卷积没办法更好的复用点值，还是写方块贡献的吧。。

实验性的代码

题意：已知 $f=f\cdot \operatorname{Xorshift}(f)\cdot z+c$ 中的 $c$ 和 $\operatorname{Xorshift}$ 函数，求系数。

http://120.27.222.204:12243/submission/113565 我抄了一个论文伪代码（参考文献 4 ），可以看到没有使用半在线算法（但是倍增的方式和划分小正方形的方式是相同的），而仅仅实现了一个 next 方法，效率较低因为半在线算法显然是可以复用一些点值的（可否跨越倍增长度复用呢？），但是这种实现大约只需额外不超过 10 行的代码量，如同 fjzzq2002 在（参考文献 3 ）中所说的，迭代进行的在线卷积应用于一些类似的生成函数是几乎没有编写难度的，但因本人能力有限，不能实现 fjzzq2002 那么漂亮的模板，只能一个个自己写递推把系数放进去。

另外值得注意的是如果提前知道所需要的长度，那么应该可以只计算正方形中的下三角形，这可能可以节省一些计算量。

对于幂级数指数函数的实验性代码（用了一些面相对象方法）：https://judge.yosupo.jp/submission/57070 最慢的点 1228 ms 实现简单。https://judge.yosupo.jp/submission/57078 上文叙述的基础算法，复用了一些点值，最慢的点 697 ms 。

烷基计数 https://loj.ac/s/1232785 706 ms 为三个同时进行的在线卷积。

P6613 一阶微分方程 https://www.luogu.com.cn/record/56435339 1.1 s 两个同时进行的在线卷积。

我觉得 2 叉分治（倍增）的优势在于其方便复用点值和编写，而多叉分治如何精细的复用点值可能在实现上需要更多的努力，但是毫无疑问效率会更高。

最后补一个多项式乘法模板 https://uoj.ac/submission/504721 1568ms 系数均在线给出，可以看到大致符合 $O(n\log^2 n)$ 的时间。

参考文献

• Elegia and Athekatelan. 信息学竞赛中的⽣成函数计算理论框架.（包含半在线及在线卷积）
• Elegia 的讲课 视频 约 50 分钟左右（半在线卷积的具体实现及常见幂级数算法表示为半在线卷积， $O\left(\frac{n\log ^2n}{\log \log n}\right)$ ）
• fjzzq2002. 一个更好的多项式模板. （算法实现）
• Joris van der Hoeven. Relax, but Don't be Too Lazy. （ $O(n\log^2n)$ 的在线卷积（易于实现））
• Joris van der Hoeven. New algorithms for relaxed multiplication. （（半）在线卷积）